Solo para Entendidos
Related Articles
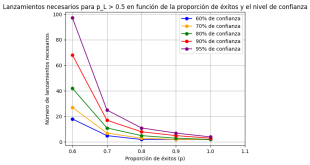
Desdoblando 3x en 2x+x, nos permite después aplicar la identidad de la suma
\(sin(3*x) = sin (2*x + x) \)Según la identidad de la suma
\(\sin(\alpha+\beta)=\sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta \)resulta entonces:
\(= sin (2*x)* cos (x) + cos (2*x)* sin(x) \)Según la identidad de ángulo doble
\(\cos(2 \alpha) = \cos^2 \alpha – \sin^2 \alpha = 1 – 2 \cdot \sin^2 \alpha = 2 \cdot \cos^2 \alpha – 1 \) \(\sin(2 \alpha) = 2 \sin \alpha \cdot \cos \alpha\)resulta entonces
\(= 2 *sin(x)* cos(x)* cos (x) + (1 – 2 *sin(x)^2) * sin(x) \)Distributiva del último término
\(= 2 *sin(x)* cos(x)*cos(x) + sin(x) – 2 *sin(x)^3\)reagrupando
\(= 2 *sin(x)* cos(x) ^2+ sin(x) – 2 * sin(x)^3\)Dado que
\(\sin^2 \alpha + \cos^2 \alpha= 1\) \(= 2 *sin(x)* (1 – sin(x)^2) + sin(x) – 2 * sin(x)^3\)Propiedad distributiva y agrupando
\(= 2 *sin(x) – 2 *sin(x)^3 + sin(x) – 2 * sin(x)^3 \)Agrupando
\(sin(3*x) = 3 *sin(x) – 4* sin(x)^3\)
