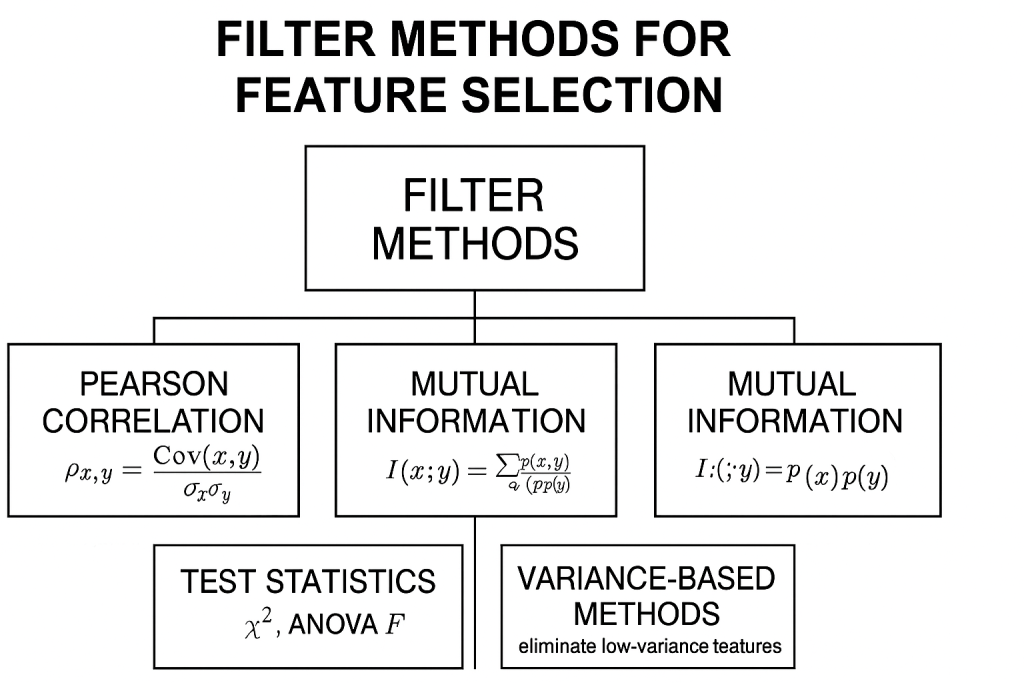
1. Introducción y Justificación
La selección de características es una etapa fundamental en el preprocesamiento de datos para machine learning, especialmente en contextos de alta dimensionalidad como el financiero. Los métodos de filtro constituyen una clase de técnicas diseñadas para seleccionar un subconjunto informativo de variables (features) evaluando únicamente propiedades estadísticas intrínsecas de cada variable con respecto a la variable objetivo. Esta selección ocurre independientemente de cualquier modelo predictivo específico y es previa a la etapa de entrenamiento de modelos.
La motivación esencial de los métodos de filtro reside en dos principios:
- Eficiencia computacional: permiten reducir la dimensionalidad de los datos de entrada de forma muy rápida y escalable, siendo ideales como primera criba en datasets con miles de variables.
- Reducción de ruido y riesgo de sobreajuste: al eliminar variables irrelevantes o casi constantes, mejoran la interpretabilidad y pueden favorecer la capacidad de generalización de los modelos posteriores【Chandrashekar & Sahin, 2014】.
En el ámbito de finanzas y trading algorítmico, donde el volumen de datos y la cantidad de indicadores derivados (lags, medias móviles, scores de volatilidad, macro, sentimiento, etc.) puede ser extremadamente alto, los métodos de filtro son una herramienta imprescindible en el pipeline de modelado.
2. Fundamento Matemático y Tipos de Criterios de Filtro
2.1. Definición Formal
Dado un conjunto de datos ![]() con
con ![]() (donde
(donde ![]() es el número total de características) y
es el número total de características) y ![]() la variable objetivo (puede ser categórica, continua, etc.), el objetivo de un método de filtro es asignar un score de relevancia
la variable objetivo (puede ser categórica, continua, etc.), el objetivo de un método de filtro es asignar un score de relevancia ![]() a cada característica
a cada característica ![]() , de modo que se pueda ordenar y seleccionar un subconjunto
, de modo que se pueda ordenar y seleccionar un subconjunto ![]() de mayor relevancia para el problema.
de mayor relevancia para el problema.
La función ![]() puede basarse en distintos principios estadísticos, que veremos en detalle.
puede basarse en distintos principios estadísticos, que veremos en detalle.
2.2. Principales Criterios Estadísticos
2.2.1. Correlación de Pearson
- Definición:
Para problemas de regresión (o clasificación binaria codificada como 0/1), la correlación de Pearson mide la asociación lineal entre la característica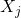 y la variable objetivo
y la variable objetivo 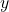 :
: ![Rendered by QuickLaTeX.com ρXj,y=Cov(Xj,y)σXjσy=E[(Xj−μXj)(y−μy)]σXjσy\rho_{X_j, y} = \frac{\mathrm{Cov}(X_j, y)}{\sigma_{X_j} \sigma_y} = \frac{\mathbb{E}[(X_j - \mu_{X_j})(y - \mu_y)]}{\sigma_{X_j} \sigma_y}ρXj,y=σXjσyCov(Xj,y)=σXjσyE[(Xj−μXj)(y−μy)]](https://www.soloentendidos.com/wp-content/ql-cache/quicklatex.com-f7598e847b2dcbcff14d08138e996e4b_l3.png) donde
donde 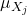 y
y 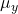 son las medias y
son las medias y 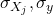 las desviaciones estándar.
las desviaciones estándar. - Interpretación:
![Rendered by QuickLaTeX.com \rho_{X_j, y} \in [-1, 1]](https://www.soloentendidos.com/wp-content/ql-cache/quicklatex.com-23229b53d45b0272dbcff933ee4d58fd_l3.png) . Se toma el valor absoluto
. Se toma el valor absoluto 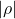 para ranking: un valor alto (cerca de 1) indica fuerte asociación lineal (positiva o negativa).
para ranking: un valor alto (cerca de 1) indica fuerte asociación lineal (positiva o negativa). - Ventajas y limitaciones:
- Muy rápido y fácil de computar incluso en datasets masivos.
- Limitación: solo detecta relaciones lineales. Variables relevantes no linealmente relacionadas con
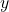 quedarán fuera.
quedarán fuera.
- Aplicación financiera:
En trading, es común calcular la correlación entre indicadores técnicos y el retorno futuro para seleccionar los más alineados a la señal objetivo (ej. momentum, RSI, etc.).
2.2.2. Información Mutua (Mutual Information, MI)
- Definición:
La información mutua entre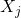 e
e 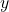 mide la reducción de incertidumbre en
mide la reducción de incertidumbre en 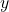 al observar
al observar 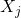 :
:  Se calcula sobre variables discretas o continuizadas; para variables continuas se usan estimadores de entropía diferencial (basados en histogramas, k-NN, etc.).
Se calcula sobre variables discretas o continuizadas; para variables continuas se usan estimadores de entropía diferencial (basados en histogramas, k-NN, etc.). - Interpretación:
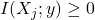 . Un valor mayor indica mayor dependencia (no necesariamente lineal).
. Un valor mayor indica mayor dependencia (no necesariamente lineal).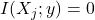 si y solo si
si y solo si 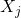 e
e 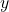 son independientes.
son independientes.
- Ventajas y limitaciones:
- Capta relaciones no lineales.
- Es más robusto ante variables con relaciones complejas, frecuentes en series financieras.
- Limitación: estimar la información mutua en variables continuas y con pocos datos puede introducir sesgo o alta varianza.
- Implementación moderna:
En scikit-learn, funciones comomutual_info_classifomutual_info_regressionimplementan estimadores eficientes de MI con el método de Kraskov, adaptados a grandes volúmenes de datos.
2.2.3. Estadísticos de Prueba
- Chi-cuadrado (
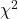 ):
):
Utilizado para variables categóricas/discretas en problemas de clasificación. Se compara la distribución observada de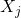 en las clases frente a la esperada por azar. Una estadística alta indica asociación significativa.
en las clases frente a la esperada por azar. Una estadística alta indica asociación significativa. - F-ANOVA:
Para problemas de clasificación, mide si la media de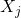 difiere significativamente entre las clases. F=Variabilidad entre gruposVariabilidad dentro de gruposF = \frac{\text{Variabilidad entre grupos}}{\text{Variabilidad dentro de grupos}}F=Variabilidad dentro de gruposVariabilidad entre grupos Un valor
difiere significativamente entre las clases. F=Variabilidad entre gruposVariabilidad dentro de gruposF = \frac{\text{Variabilidad entre grupos}}{\text{Variabilidad dentro de grupos}}F=Variabilidad dentro de gruposVariabilidad entre grupos Un valor 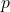 -value bajo (usualmente
-value bajo (usualmente 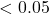 ) indica que la característica es relevante para discriminar entre clases.
) indica que la característica es relevante para discriminar entre clases. - Ventajas:
- Sencillos de interpretar, ideales para datasets con variables mixtas.
- Proveen control estadístico para descartar features que no son significativamente distintas entre clases.
- Limitaciones:
- Poca robustez a relaciones no lineales o estructuras complejas de interacción.
2.2.4. Métodos basados en varianza y entropía
- Varianza nula o casi nula:
Características con muy baja varianza (prácticamente constantes) se eliminan porque no aportan diferenciación predictiva.
Var(Xj)≈0 ⟹ Xj inútil para predecir y\operatorname{Var}(X_j) \approx 0 \implies X_j \text{ inútil para predecir } yVar(Xj)≈0⟹Xj inútil para predecir y - Entropía baja:
Variables categóricas con un único valor dominante (alta asimetría en la distribución) suelen ser poco útiles. - Implementación:
Herramientas comoVarianceThresholdde scikit-learn permiten automatizar este paso.
3. Procedimiento Estándar de los Métodos de Filtro
Un pipeline típico incluye los siguientes pasos, fácilmente automatizables:
- Cálculo del criterio de importancia:
Se computa el score de relevancia elegido (correlación, MI, estadístico de prueba, etc.) para cada característica
elegido (correlación, MI, estadístico de prueba, etc.) para cada característica 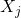 en el conjunto de entrenamiento.
en el conjunto de entrenamiento. - Ranking y ordenamiento:
Las características se ordenan de mayor a menor según el score .
. - Selección del subconjunto:
Se escoge un umbral (top-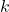 , umbral absoluto, criterio estadístico) para seleccionar las características con mayor relevancia.
, umbral absoluto, criterio estadístico) para seleccionar las características con mayor relevancia. - Eliminación opcional de redundancia:
Si el análisis identifica variables altamente correlacionadas entre sí en el subconjunto seleccionado, se pueden eliminar las redundantes para evitar multicolinealidad, usando métodos como análisis de clusters de correlación, VIF (Variance Inflation Factor), etc. - Validación (opcional):
Se evalúa si el subconjunto elegido conserva el desempeño predictivo esperado en un conjunto de validación. En contexto financiero, se recomienda validación temporal (ej. walk-forward).
4. Ventajas de los Métodos de Filtro
- Escalabilidad extrema:
Aptos para datasets con decenas de miles de features (por ejemplo, todos los lags posibles de series financieras de alta frecuencia). - Desacoplamiento del modelo:
El mismo subconjunto seleccionado puede ser utilizado en cualquier modelo (LightGBM, redes neuronales, regresión, etc.). - Bajo riesgo de sobreajuste:
Al no usar el modelo como función objetivo, no optimizan para los datos de entrenamiento en exceso, disminuyendo el riesgo de seleccionar variables que solo son útiles por azar.
5. Limitaciones Fundamentales
- Ignoran interacciones y sinergias:
Dado que la mayoría son univariantes, pueden omitir variables que solo muestran relevancia en interacción (por ejemplo, la diferencia entre dos indicadores que por sí solos no predicen el retorno, pero en conjunto sí). - Posibilidad de selección de proxies espurios:
Una variable puede mostrar alta correlación con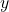 por simple coincidencia temporal (relación espuria, problema clásico en series financieras).
por simple coincidencia temporal (relación espuria, problema clásico en series financieras). - No consideran redundancia en el objetivo final:
Si hay variables redundantes (altamente correlacionadas entre sí), un filtro típico seleccionará varias, lo que puede perjudicar modelos sensibles a la multicolinealidad (regresión lineal, LASSO, etc.). - Sesgos por no linealidad y distribución:
El score de correlación ignora relaciones no lineales; la MI depende de una buena estimación de las distribuciones, que no siempre es trivial.
6. Ejemplo Profundo: Aplicación Práctica en Finanzas
Caso Simulado: Selección de Indicadores en Trading Diario
Suponga un conjunto de datos simulado con ![]() días de cotizaciones, con las siguientes características:
días de cotizaciones, con las siguientes características:
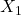 = Retorno del día anterior (
= Retorno del día anterior (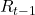 )
)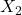 = Diferencia de medias móviles (MA5 – MA20) (momentum)
= Diferencia de medias móviles (MA5 – MA20) (momentum)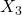 = Volatilidad a 10 días
= Volatilidad a 10 días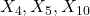 = Ruido aleatorio (variables sin relación con
= Ruido aleatorio (variables sin relación con 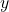 )
)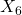 = Sentimiento Twitter (dummy no correlacionado)
= Sentimiento Twitter (dummy no correlacionado)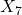 =
= 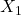 + ruido pequeño (versión redundante)
+ ruido pequeño (versión redundante)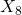 =
= 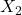 + ruido pequeño (versión redundante)
+ ruido pequeño (versión redundante)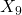 = Suma de retornos últimos 3 días
= Suma de retornos últimos 3 días
Objetivo: ![]()
Cálculo de scores de filtro:
- Correlaciones: ρX1,y≈0.71ρX7,y≈0.51ρX9,y≈0.49ρX2,y≈0.41ρX3,y≈0.13ρX4,y,ρX5,y,ρX10,y≈0
ρX1,yρX7,yρX9,yρX2,yρX3,yρX4,y,ρX5,y,ρX10,y≈0.71≈0.51≈0.49≈0.41≈0.13≈0 El ranking muestra que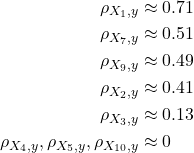
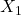 ,
, 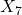 ,
, 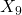 ,
, 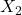 son los más correlacionados.
son los más correlacionados. - Información mutua (estimada por k-NN): I(X1;y)≈0.38I(X9;y)≈0.16I(X2;y)≈0.09I(X4;y),I(X5;y),I(X10;y)≈0
I(X1;y)I(X9;y)I(X2;y)I(X4;y),I(X5;y),I(X10;y)≈0.38≈0.16≈0.09≈0 De nuevo,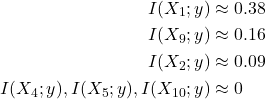
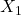 lidera, con
lidera, con 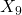 y
y 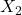 detrás.
detrás.
Selección resultante:
Un método filtro que selecciona las 4 primeras variables según correlación/MI elegiría ![]() .
.
Discusión crítica:
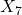 es casi redundante de
es casi redundante de 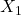 ; incluir ambas no mejora y puede empeorar la interpretación.
; incluir ambas no mejora y puede empeorar la interpretación.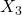 (volatilidad) tiene score bajo, pero podría ser importante en un régimen de alta volatilidad, lo cual un método filtro univariante puede pasar por alto.
(volatilidad) tiene score bajo, pero podría ser importante en un régimen de alta volatilidad, lo cual un método filtro univariante puede pasar por alto.- Las variables de ruido correctamente aparecen en último lugar.
Código Python ilustrativo:
import numpy as np
import pandas as pd
from sklearn.feature_selection import mutual_info_classif
# Supongamos un DataFrame df con las variables descritas y una columna 'y'
correlations = df.corr()['y'].abs().sort_values(ascending=False)
print("Correlaciones con y:")
print(correlations)
mi = mutual_info_classif(df.drop('y', axis=1), df['y'], discrete_features=False)
mi_series = pd.Series(mi, index=df.columns[:-1]).sort_values(ascending=False)
print("Información mutua con y:")
print(mi_series)
# Selección top-4
selected = mi_series.head(4).index.tolist()
print("Variables seleccionadas:", selected)
7. Estado del Arte: Avances Recientes y Mejoras Modernas
- Filtros multivariantes:
Aunque la mayoría de métodos clásicos son univariantes, se han propuesto criterios multivariantes como mRMR (minimum Redundancy Maximum Relevance), que selecciona variables maximizando la MI con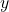 y minimizando la redundancia mutua entre variables elegidas.
y minimizando la redundancia mutua entre variables elegidas. ![Rendered by QuickLaTeX.com maxS⊆F,∣S∣=k[∑Xj∈SI(Xj;y)−λ∑Xj,Xk∈S,j≠kI(Xj;Xk)]\max_{S \subseteq \mathcal{F}, |S|=k} \left[ \sum_{X_j \in S} I(X_j;y) - \lambda \sum_{X_j,X_k \in S, j\neq k} I(X_j;X_k) \right]S⊆F,∣S∣=kmaxXj∈S∑I(Xj;y)−λXj,Xk∈S,j=k∑I(Xj;Xk)](https://www.soloentendidos.com/wp-content/ql-cache/quicklatex.com-881abe28ca2eb2fa1e12f2c574c67601_l3.png) Esta técnica ha mostrado mejoras sobre filtros simples, especialmente en dominios de alta colinealidad, como finanzas【Peng et al., 2005】.
Esta técnica ha mostrado mejoras sobre filtros simples, especialmente en dominios de alta colinealidad, como finanzas【Peng et al., 2005】. - Feature selection con autoencoder:
Se han desarrollado métodos basados en autoencoders supervisados que asignan puntuaciones de importancia a features según su reconstrucción y relevancia para la predicción, permitiendo filtrar features irrelevantes. Ejemplo: Supervised Autoencoder Feature Selector (SAFS)【Li et al., 2021】. - Evaluación de estabilidad:
En finanzas, se recomienda realizar selección de características en ventanas temporales deslizantes y comparar la estabilidad de los subconjuntos elegidos. Variables que aparecen consistentemente importantes en distintos períodos son candidatas robustas. - Filtros basados en gráficos:
Para conjuntos masivos de datos, se usan filtros basados en grafos de similitud (selección por centralidad, detección de comunidades) para elegir subconjuntos no redundantes de alto impacto.
8. Conclusión y Recomendaciones Prácticas
Los métodos de filtro deben considerarse como el primer y esencial paso de reducción de dimensionalidad, especialmente en entornos de datos de alta dimensión como el financiero. Su rapidez y facilidad de implementación los hacen ideales para descartar ruido y concentrar los esfuerzos de modelado en las variables realmente informativas. Sin embargo, deben ser complementados con análisis de redundancia y, eventualmente, métodos de selección más avanzados (envoltorio, integrados, SHAP, etc.), para garantizar que el subconjunto final sea no solo relevante, sino también parsimonioso y robusto frente a cambios de régimen.
El uso combinado de filtros univariantes y multivariantes, junto con validación cruzada y experticia de dominio, constituye la mejor práctica en la actualidad para la selección inicial de variables en problemas de trading algorítmico con LightGBM y otros algoritmos de machine learning.
Referencias seleccionadas
Li, J. et al. (2021). Supervised autoencoder-based feature selection for high-dimensional data. Pattern Recognition, 113, 107840.
Chandrashekar, G., & Sahin, F. (2014). A survey on feature selection methods. Computers & Electrical Engineering, 40(1), 16–28.
Peng, H., Long, F., & Ding, C. (2005). Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(8), 1226–1238.
 Solo para Entendidos
Solo para Entendidos