Problema de Disolución – Ecuaciones Diferenciales por Variación de Parámetros

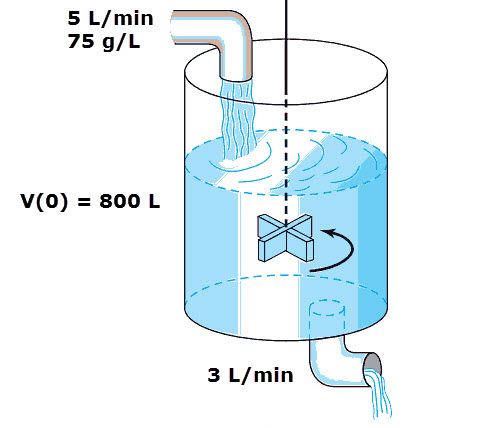
Tenemos un tanque inicialmente con 800 litros de agua pura al cual le ingresa un flujo de solución salina con concentración de 75 gramos por litro, a un ritmo de 5 litros por minuto y salen 3 litros por minuto. Deseamos conocer la ecuación de concentración del tanque en función del tiempo.

V₀ = 800 l, I = 5 l/min (75 g/l) , O = 3 l/min, x_(t) = total gramos de sal en el tanque

V_(t) = litros totales = 800 + 2t (ya que hay 800 iniciales y entran 5 y salen 3 por minuto)  (1)

Concentración se define como cantidad de sal sobre el volumen total, x_(t)/v_(t)

La cantidad de sal de entrada será el caudal de entrada por la concentración de la solución de entrada, es decir, 75 g/l a 5 l/m = 375 g/min.

La cantidad de sal de salida será el caudal de salida por la concentración de la solución de salida, es decir, 3 l/min por la concentración que depende del tiempo. x_(t)/v_(t) . 3 l/min, reemplazando (1)

\(Salida = \frac{3x}{800 + 2t} . g/min\).

La variación de sal en función del tiempo será lo que entra menos lo que sale:

\(\frac{dx}{dt} = 375  . g/min – \frac{3x}{800 + 2t} .  g/min\).

Rearreglando la ecuación a la forma

\(\dot{x} + p(t)x = q(t)\).

\(\frac{dx}{dt} + \frac{3}{800 + 2t} . x . g/min = 375 . g/min \).

Ya que q(t) es distinto de cero, esta ecuación es NO homogénea.

Paso 1: Resolviendo la ecuación diferencial homogénea asociada

\(\frac{dx}{dt} + \frac{3}{800 + 2t} . x . g/min = 0 \).

Resolviendo por separación de variables,

\( ln(x) = \int\frac{dx}{dt} = \int\frac{-3dt}{800 + 2t} = \frac{-3}{2} ln(400+t) + C_1\).

\( ln(x) = \frac{-3}{2} ln(400+t) + C_1\).

\( x = e^{C_1}* (400+t) ^{\frac{-3}{2}}\).

eligiendo C₁ = 0, resulta

\( x = (400+t) ^{\frac{-3}{2}}\).

Paso 2: Substituyendo x = U(t) Xh(t) y resolviendo U

\(\frac{d}{dt}(UX_h) + \frac{3}{800 + 2t} (UX_h) = 375 \).

U y X_h dependen de t por lo que en la primer derivada se debe aplicar la regla de la cadena de derivación.

\(\dot{U}(400+t)^{\frac{-3}{2}}+U(\frac{-3}{2}(400+t)^{\frac{-5}{2}}) + \frac{3}{800 + 2t} (UX_h)\).

Los últimos dos términos se cancelan resultando,

\(\dot{U} = 375 (400+t) ^{\frac{3}{2}}\).

\(\dot{U} = 375 (400+t) ^{\frac{3}{2}}\).

\(U = 150 (400+t) ^{\frac{5}{2}}\).

Paso 3: Multiplicando para obtener x(t) = U(t) Substituyendo x = U(t) * Xn(t)

\(X(t) = [150 (400+t) ^{\frac{5}{2}}+C_2] * (400+t) ^{\frac{-3}{2}}\).

\(X(t) = 60000+150t+\frac{C_2}{ (400+t) ^{\frac{3}{2}}}\).

Paso 4: Ajustando a la condición inicial de x(0) = 0

\(0 = 60000+\frac{C_2}{ 400 ^{\frac{3}{2}}}\).

C₂ = –4.8.10⁸

Finalmente

\(X(t) = 60000+150t+\frac{-4.8.10^8}{ (400+t) ^{\frac{3}{2}}}\).

 

Resolución de ecuaciones diferenciales por factor de integración