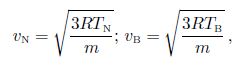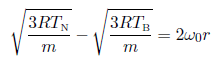Solo para Entendidos
Related Articles
El radiómetro de Crookes es un instrumento diseñado originalmente para medir la presión de la radiación electromagnética. Consta de cuatro pequeños cuadrados puesto es los extremos de un aspa que pivota sobre una punta metálica fina sobre la que puede girar. Las caras de los cuadrados están pintadas de negro por un lado y de blanco por el otro lado y estos están colocados de tal forma que las superficies blancas y negras se van alternando en los cuatro. En otros radiómetros un lado está pintado de negro y el otro lado es de metal pulido, sin pintar. Todo el sistema se coloca dentro de un bulbo de vidrio en el que se ha hecho un vacío suficientemente alto.
En el caso de los radiómetros de Crookes, se tiene que ambos giran muy deprisa cuando son iluminados por una bombilla de resistencia a alta temperatura, que produce luz visible, aunque se observa que gira más lentamente el radiómetro cuyas superficies están pintadas de blanco y de negro en relación con el radiómetro uno de cuyos lados es de metal pulido.
Cuando ambos radiómetros son iluminados por una lámpara de infrarrojos, sólo gira el radiómetro cuyas superficies opuestas a las pintadas de negro están bruñidas. El otro radiómetro, el que tiene ambos lados pintados, aunque uno de ellos sea de blanco, permanece en reposo.
¿Cómo se relacionan estas experiencias de los radiómetros con las experiencias de Leslie y el Teorema de Kirchhoff?
Aparentemente sólo el radiómetro con caras pulidas debería girar, pero no el radiómetro con caras pintadas de blanco. Lo que se tiene en relación con las experiencias del cubo de Leslie y del radiómetro de Crookes no es contradictorio una vez se analiza correctamente. En primer lugar, la ley de Kirchhoff anteriormente citada se refiere a superficies que emiten y absorben a la misma temperatura (mismas longitudes de onda de las radiaciones absorbidas y emitidas). Si bien las superficies pintadas de negro emiten y absorben bien radiación a cualquier temperatura, no sucede lo mismo con las superficies pintadas de blanco. Estas últimas absorben bien la radiación infrarroja –y la emiten también bien, lo que sucede a bajas temperaturas–, pero absorben mal la radiación visible –y también la emiten mal, lo que sucede a altas temperaturas–. A 100 C ambas superficies emiten en la zona de los infrarrojos y casi lo mismo, por lo que cuando se ponen en un radiómetro y son iluminadas con radiación infrarroja, éste prácticamente no gira. A temperaturas próximas a los 3000 K, temperatura de un filamento de bombilla, la superficie negra absorbe toda la radiación , pero la superficie blanca apenas absorbe la radiación visible. Si ambas superficies del cubo de Leslie se pusieran a esta temperatura se observaría que la superficie negra emite mucho más que la blanca. Por tanto, cuando el radiómetro es iluminado por la bombilla de luz visible, la superficie pintada de negro absorbe más la radiación que la pintada de blanco, las moléculas de aire en contacto con esta superficie alcanzan mayor temperatura que las moléculas de la superficie pintada de blanco y golpean con mayor velocidad dicha superficie negra, por lo que el radiómetro gira con las superficies negras huyendo de la luz. Puesto que las superficies pulidas siempre absorben mal la radiación a cualquier temperatura, también la emiten mal a cualquier temperatura. Por esta razón, el radiómetro con superficies negras y pulidas gira tanto al ser iluminado por radiación visible como al ser iluminado con radiación infrarroja.
¿Cómo funciona un radiómetro de Crookes?
Este análisis indica que el radiómetro no funciona en caso de un vacío perfecto. En ausencia de moléculas de aire en el radiómetro nada material golpea las superficies y la presión de radiación no es suficiente como para vencer el pequeño rozamiento del pivote que gira5. En ciertas aplicaciones, los fotones se consideran como partículas de ‘masa’ h/c2 y momento lineal p = h/c, siendo su frecuencia, h la constante de Planck y c la velocidad de la luz.
Considérese que dos caras de las aspas de un radiómetro son iluminadas con luz de una única frecuencia y que dichos fotones son absorbidos por completo en la cara pintada de negro y que no son absorbidos (rebotan) en la cara pulida o pintada de blanco. Se tiene entonces que la variación de momento lineal en la cara pintada de negro sería de +h/c, mientras que es de -2h/c en las caras pulidas o blancas. Aparecería entonces una fuerza neta y un momento angular que haría que las superficies pulidas o blancas se alejarían de la fuente de luz y las superficies negras se acercarían a la fuente de luz. Experimentalmente se observa justamente lo contrario, con las caras pintadas de negro alejándose de la fuente de luz. Dos radiómetros como los anteriores son colocados en el interior de un frigorífico. Aunque hay descripciones que indican que gira en sentido contrario al sentido de cuando es iluminado, esto no se ha observado.
Una vez enfriados durante tiempo suficiente, son puestos en el exterior, a temperatura ambiente. Entonces giran en sentido normal, pues la superficie negra se calienta algo más rápido que la superficie blanca. Dos radiómetros como los anteriores se colocan enfrente de un fuego. Después de un cierto tiempo, se ponen en otro lugar de la habitación, casi a oscuras, lejos del fuego. El pintado de blanco y negro, que ha dejado de girar enfrente del fuego, comienza a girar en sentido contrario. La superficie pintada de negro se enfría más rápido que la superficie pintada de blanco –sólo un poco más rápido–, lo suficiente como para que durante un corto periodo de tiempo gire en sentido contrario6. Aunque en la región de los infrarrojos las superficies pintadas de blanco emiten y absorben tanto como las superficies pintadas de negro (experiencias de Leslie), no sucede lo mismo en la zona del visible y las superficies blancas reflejan mucho más la radiación que las superficies negras, por lo que estas alcanzan temperaturas más altas. En consecuencia, las moléculas de aire próximas a la superficie negra tienen una velocidad media mayor que las moléculas de aire próximas a las superficies blancas.
Cuando se dispone de dos tipos de radiómetros, uno con las caras plateadas y pintadas de negro y el otro con una cara pintada de blanco y la otra pintada de negro, se observa que frente a los infrarrojos el primero gira más rápido que el segundo, que apenas gira. Frente a la luz visible, o con bastante componente visible, siempre gira más rápido el que tiene la cara más reflectante, la plateada. Suponiendo que las moléculas se mueven todas con la velocidad media, vN en el caso de las moléculas próximas a la superficie negra y vB en el caso de las moléculas próximas a la superficie blanca, puesto que las superficies negras se alejan de la luz con velocidad u, las moléculas que golpean esa superficie lo hacen con una variación de momento de 2m(vN −u) (o lo que es lo mismo, respecto de las moléculas que golpean lo que interesa es su velocidad relativa respecto de la superficie). Puesto
que en la unidad de tiempo dt, aproximadamente 1/6 del número de moléculas contenidas en un volumen A(vN −u)dt, A(vN −u)ndt, siendo A la sección de la superficie y n la densidad de partículas en el interior del radiómetro, chocarán contra la superficie, se tiene que la variación del momento viene dada por
dpN = 1/3mAn(vN − u)2dt –> dp/dt = FN = 1/3mAn(vN − u)2
Por tanto, la presión ejercida sobre la superficie negra será
PN = FN / A = 1/3mn(vN − u)2
Razonando del mismo modo sobre la superficie blanca, teniendo en cuenta que se aproxima a la luz con velocidad u, por lo que se aproxima a las moléculas, se tiene que en la unidad de tiempo dt, 1/6 del número de moléculas contenidas en un volumen A(vB + u)dt, An(vB + u)dt, golpearán esa superficie y, finalmente,
PB = FB / A = 1/3 mn(vB + u)2
Puesto que la fuerza neta que actúa sobre superficie del aspa es (en valor absoluto)
FT = FN − FB ,
y el momento del par de fuerzas que se origina es
τ = 2FTr = Iω = I u/r
siendo I = mr2 el momento de inercia del aspa. Por tanto,
2FT = Mu
siendo M = AS la masa de las superficies del radiómetro y S su
densidad superficial de masa. Cuando se alcanza el régimen estacionario la velocidad angular es constante, y también la velocidad lineal, por lo que la fuerza neta que se ejerce sobre cada superficie es nula. En ese caso, con u
vN − u = vB + u –> vN − vB = 2u = 2ωr
De acuerdo con la teoría cinética de los gases
y
Para un radiómetro con r = 0.02 m, TB = 300 K y !0 = 10×2 = 62.8 rad s−1, y con m = 29×10−3 kg mol−1, se tiene que (sin considerar la fricción)
TN ~ 303K
Con sólo lograr que se establezca esta pequeña diferencia de temperaturas entre ambas caras se puede conseguir que las aspas del radiómetro giren a gran velocidad.
