En los últimos tiempos se habló muchísimo sobre el descubrimiento o medición precisa del CMB Cosmic Microwave Background – el fondo cósmico de microondas. La razón es que este, daría evidencia de lo que se supone ocurrió segundos después del Big Bang y así dar prueba de ello.
El CMB fue inicialmente medido por casualidad al utilizar una antena en los laboratorios Bell la cual recibía “ruido” en todas dirección el cual finalmente se adjudicó al CMB que es el vestigio dejado por el Big Bang.
La teoría del Big Bang establece que en los primeros segundos después, la alta densidad y energía posibilitaron la fusión y creación de elementos, pero los fotones existentes tenían energía suficiente para arrancar los electrones de los hidrógenos que se formaban.
Esta energía se fue disipando con la expansión hasta que no lograron romper el hidrógeno el cual también formó helio y para ese entonces, unos 90 segundos después del Big Bang, comenzó la reacción de fusión dejando un 25% de helio y un 75% de hidrógeno y algunos rastros de litio y deuterio. Relación que aún predomina en la masa actual del universo. Aunque las estrellas siguen fusionando hidrógeno en helio, no llegan a explicar la abundancia actual del helio el cual fue producido al comienzo de los tiempos.
Por otro lado, los fotones de alta energía son capaces de convertirse en masa según E=mc2. Así un fotón puede crear un electrón y un positrón los cuales después, debido a la alta densidad, se aniquilan produciendo nuevamente un fotón.
La abundancia de energía respecto de la masa es de 1.109 fotones por cada partícula. Posteriormente los fotones van perdiendo energía y ya no logran crear más partículas. Aparentemente una en un billón no se volvieron a aniquilar.
Al no existir antimateria, se sigue buscando una reacción por la cual las partículas se aniquilen con las antipartículas y quede 1:1.109 partes de materia. Con eso se podría justificar la materia del universo.
¿Cuál sería entonces la edad, densidad y temperatura del universo al momento de que los fotones produjeran electrones-positrones?
La energía del fotón debe ser suficiente para producir ambas partículas,
\(m_e = m_p = 9.1*10^{-31} kg\) ; \(E=mc^2\)
\(E=1.6*10^{-13} J = 10^6 eV\)
Actualmente la energía promedio de un fotón está en 10-3 eV, por tanto:
\(E_{(t)} = \frac{10^{-3}}{a_{(t)}}\) => \(a(t) = 10^{-9}\)
Por lo que el universo era mil millones de veces más denso de lo que es ahora
\(z = \frac{1-a_{(t)}}{a_{(t)}} = 10^9\)
La densidad es inversamente proporcional al cubo del factor de escala y la densidad aproximada actual es de 5*10-28kg/m3
\(\rho \propto \frac{1}{a_{(t)}^3}\) ; \(\rho_0 \sim 5*10^{-28} kg/m^3\)
\(\rho \simeq 0.5 kg/m^3\)
Otra manera de llegar a a(t) es: Si el Helio se produce a temperaturas de de 109 K y densidades de 10-2 kg/m3 entonces:
el factor de escala para el momento en que la temperatura del universo era suficiente para que se fusionara el helio resulta de la relación entre la densidad actual y la de ese momento, elevado a la 1/3. Concluyendo:
\(a_{(t)} \simeq (\frac{\rho_0}{\rho_{He}})^{1/3} = 3.47*10^{-9}\)
La temperatura actual de ese evento se puede calcular de:
\(T_0 = a_{(t)} * T_{He} = 3.47K\)
Es decir que la temperatura de la radiación gamma resultante del evento de la síntesis del helio segundos después al Big Bang, hoy se calcula en alrededor de 3 grados Kelvin dada la pérdida de energía por la expansión del universo. Finalmente, este es el orden de temperatura del CMB.
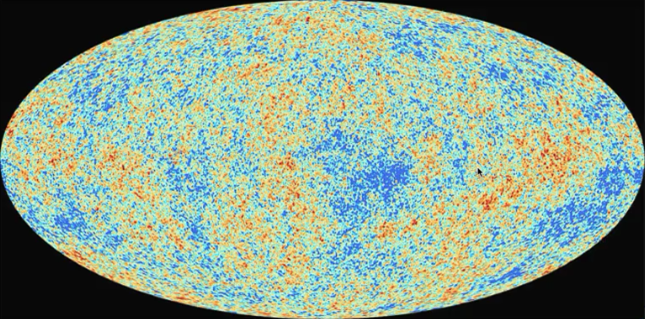
Imagen del Fondo Cósmico de Microondas (Satélite Planck – 2013)
Esta imagen muestra una homogeneidad total por debajo de una parte por 100.000. No se ven patrones claros tampoco. Por tanto hay que analizar de forma estadística la distribución así como se hace con las galaxias que muestran un pico de distribución cada 100 ó 150 megaparsecs.
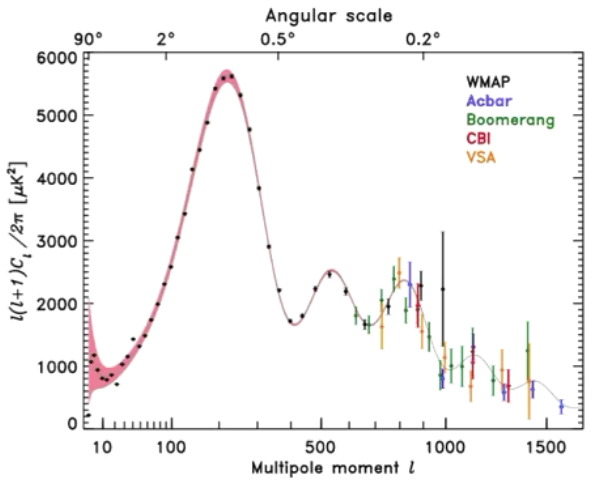
En este caso, el análisis se hace por separación angular (correlación entre dos puntos) donde se ve un pico aproximadamente 1º. Es decir que, dado por ejemplo un punto caliente, cual es la probabilidad de encontrar otro a una distancia angular determinada.
La imagen del CMB pertenece al momento en que el universo se volvió tranparente donde se formaron los átomos de Hidrógeno, antes de esto, era un plasma caliente y denso donde la materia bariónica y la luz estaban fuertemente enlazadas. Cualquier inhomogeneidad, como fluctuación térmica, se vería como una región un poco más densa y por tanto caliente donde la presión de radiación expandiría esta zona comprimiendo las zonas circundantes produciendo así una “onda de sonido” la que se propagaría a la velocidad del sonido en el plasma. Por tanto, las fluctuaciones que vemos en el CMB son las ondas primordiales de estas inhomogeneidades.
Para sustentar esta idea, veamos cuál es el alcance de cualquiera de estas ondas. Esto es la región con la cual se pueda comunicar o influir y está limitada por la distancia de horizonte. Pero la velocidad de propagación no es la velocidad de la luz, sino la del sonido en el plasma. Esta velocidad corresponde a \( \frac{1}{\sqrt[]{3}}\)
La longitud de onda resulta como la distancia de horizonte en el momento de ionización sobre la raíz de 3 o lo que es lo mismo, raíz de 3 por la velocidad de la luz por t de ionización.
\( \lambda = \frac{D_h(t_{ion})}{ \sqrt{3}} = \sqrt{3}ct_{ion}\)
Esto en unidades actuales es 200 kilo parsecs. Para calcular el ángulo, debemos calcular la distancia dada por:
\(D = 3ct_0(1 – (\frac{t_{ion}}{t_0})^{\frac{1}{3}})\) ; \(a_t = a_0(\frac{t}{t_0})^{\frac{2}{3}}\)
entonces \(D = 3ct_0(1 – \sqrt{a_{ion}})\)
Finalmente
\( \theta = 57.3 \frac{ \lambda (1 + z)}{D}\)
\(= 57.3 \frac{\sqrt{3}ct_{ion}a_{ion}^{-1}}{3ct_0(1-a_{ion}^{\frac{1}{2}})}\)
\(= 57.3 \frac{a_{ion}^{\frac{1}{2}}}{\sqrt{3}(1-a_{ion}^{\frac{1}{2}})}\)
Resultando un lambda de 0.97º que coincide con el pico de 1º del estudio estadístico confirmando que el universo es plano ya que si no lo fuera estos ángulos se verían distorcionados.
 Solo para Entendidos
Solo para Entendidos