Solo para Entendidos
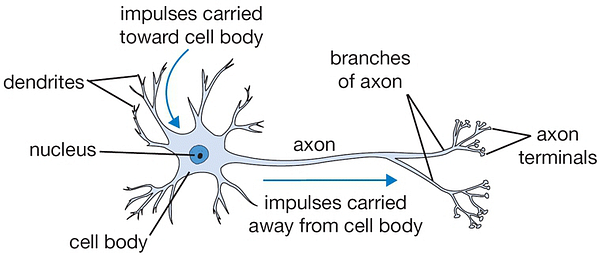
El ser humano ha tratado de recrear el funcionamiento del cerebro y proceso de aprendizaje mediante modelos computacionales llamados redes neuronales. Las neuronas son células nerviosas interconectadas entre sí que intercambian estímulos y, si la suma de estímulos que reciben rompen cierto umbral, “dispara” hacia otra neurona en forma de todo o nada, no hay términos medios.
El fin de las redes neuronales es lograr la función más preciada del cerebro, aprender. El proceso de aprendizaje del cerebro consiste en prueba y error y la retroalimentación según el resultado de un acto para así modificar el comportamiento del “circuito” al cambiar algunos parámetros (mielinización de los axones). Así es que el niño busca aceptación mirando la reacción de sus padres frente a un acto y los sentidos le producen dolor al tocar algo caliente.
Las neuronas transmiten estímulos a las siguientes mediante su axón el cual está envuelto por una vaina de mielina que se encarga de fortalecer el enlace y asegurar la correcta y rápida transmisión. Cuando se aprende algo y se lo practica con éxito, estas conexiones se refuerzan (mielinizan); si la experiencia fue pobre, la conexión se debilita.
Las neuronas reciben impulsos desde otras mediante los axones, si la suma de estos alcanza el umbral, la neurona dispara hacia la siguiente. Esta función de activación se puede modelizar mediante una función STEP, sigmoide o ReLU (Rectified Linear Unit).
El estímulo de una neurona resulta la suma de todos los estímulos Xi ponderados recibidos mediante un coeficiente Wi (weight) y si supera un umbral determinado b (threshold), esta dispara a la siguiente según un Z, función de X, W y b.
Z = ∑ Xi . Wi > b (threshold), ó
condición de disparo Z = b – ∑ Xi . Wi > 0
Definimos de forma conveniente una función P (performance) como menos un medio del cuadrado del valor absoluto de la diferencia entre el valor esperado y el obtenido por la red
P = – ½||D – Z||2
desearemos entonces maximizar esta función P según las ponderaciones W. Si tenemos un par de neuronas con W1 y W2, podemos visualizar en un gráfico de contorno la función P. Así para aproximarnos al máximo de la función P, debemos movernos en dirección del gradiente según las derivadas parciales de P respecto de W1 y W2.
Entrenar una red neuronal es variar los parámetros W y b (peso de ponderación y umbral de disparo) para que la función P (performance) sea máxima, o lo que es lo mismo, que el error sea mínimo; resultando el valor final Z cercano al deseado D, es decir que una red neuronal es una función aproximadora.
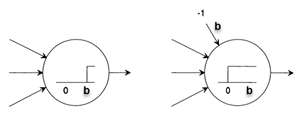Para simplificar el entrenamiento, es conveniente sacar el umbral b de la ecuación y manejar solo ponderaciones W, para eso se recurre al truco de generar una neurona extra con valor fijo -1 y con un W0 de valor T. Así en lugar de modificar el umbral, se modifica un peso como en el caso de las demás neuronas siendo esto equivalente. De esta manera la función STEP queda centrada en el eje vertical.
Adicionalmente a esto, para buscar el máximo de la función Performance, hay que igualar a cero la derivada y la función STEP no es continua por lo que no es conveniente para deriva. reemplazamos entonces la función STEP por la sigmoide la cual tienen propiedades convenientes para la derivación. Se verifica que si S es la función sigmoide, su derivada S’ = S (1 – S) con lo cual se puede hacer cálculos de sus derivadas SIN derivar ya que la derivada está expresada en términos de la función misma.
1/(1+e-z)
Computacionalmente se resuelve la búsqueda de los parámetros, en forma numérica, haciendo pequeñas variaciones de W (tal como si fuera un Newton Raphson en busca de los ceros de una función) denominado Descenso del Gradiente según:
∆Wi+1 = Wi + ∆Wi donde,
∆Wi = – learningRate x gradiente + momentum x ∆Wi-1
Estos parámetros son configurables en el Weka dentro del algoritmo Multilayer Perceptron. ∆W son las variaciones que se hace de las ponderaciones en cada iteración para ajustarse a los valores esperados de salida y el tamaño de los saltos se hacen según el parámetro momentum y learningRate en el sentido del gradiente. Así los W comienzan siendo valores aleatorios para ser ajustados con el objetivo de que converjan hacia los valores deseados en la medida en que se procesan instancias del trainning set.
Nos daremos por satisfechos cuando la función P(erformance) es máxima, pero la convergencia hacia ese estado a veces no se logra pasando una vez por los datos. Esto puede deberse a una dificultad propia de la función o los parámetros elegidos como el learning rate y el momentum (el gradiente se autocalcula).
Por esto último, se pasa otra vez el set de entrenamiento (a cada pasada se lo llama epoch o época)
Weka maneja por defecto un hidden layer y el tamaño por defecto es a = (features + clases) / 2, input es igual a features, output es igual a classes y t = features + classes.
